Standardization and Min-Max Scaling in Machine Learning and Deep Learning.
Introduction
Feature scaling is an essential preprocessing step in Machine Learning and Deep Learning. Two of the most commonly used techniques for feature scaling are Standardization and Min-Max Scaling. These methods help in transforming the data into a format that is better suited for training models, ensuring that algorithms perform optimally.
What is Standardization?
Standardization is a technique that transforms data to have a mean of zero and a standard deviation of one. This method centers the data by subtracting the mean and scales it by dividing by the standard deviation. The standardized data typically follows a normal distribution, which is crucial for algorithms that assume normally distributed input data.
Formula:
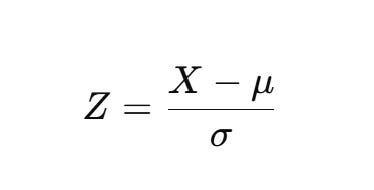
Where:
- Z is the standardized value.
- X is the original value.
- μ is the mean of the data.
- σ is the standard deviation of the data.
Example:
Consider a dataset of students’ scores:

To standardize these scores:
- Calculate the mean (μ):
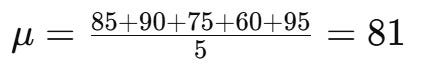
- Calculate the standard deviation (σ):
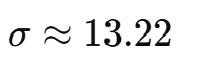
- Standardize the scores:
For Student A:
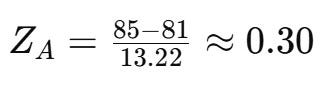
What is Min-Max Scaling?
Min-Max Scaling (also known as normalization) transforms data by rescaling it to a specific range, usually [0, 1]. This is particularly useful when the algorithm’s performance depends on the range of input data. It ensures that all features contribute equally to the result, which is crucial in algorithms sensitive to data range.
Formula:
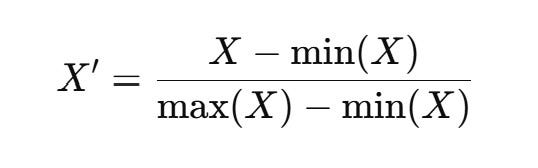
Where:
- X′′ is the scaled value.
- X is the original value.
- min(X) and max(X) are the minimum and maximum values of the dataset.
Example:
Using the same student scores:
- Identify the minimum and maximum scores:
min(X)=60
max(X)=95 - Apply Min-Max Scaling:
For Student A:
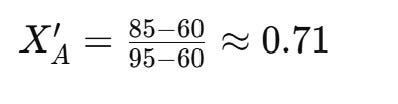
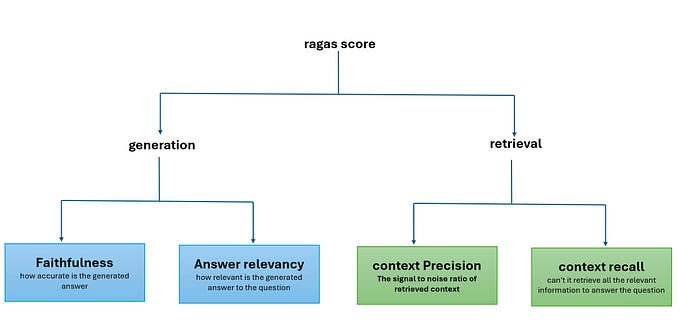
Differences Between Standardization and Min-Max Scaling
Range:
- Standardization: Transforms data to have a mean of 0 and a standard deviation of 1 without bounding the range.
- Min-Max Scaling: Scales data to a fixed range, typically [0, 1].
Sensitivity to Outliers:
- Standardization: Less sensitive to outliers as it focuses on mean and standard deviation.
- Min-Max Scaling: More sensitive to outliers since they affect the minimum and maximum values directly.
Use Cases:
- Standardization: Preferred in algorithms assuming normally distributed data, such as Logistic Regression, Linear Regression, and PCA.
- Min-Max Scaling: Used in algorithms sensitive to input data range, such as Neural Networks and K-Nearest Neighbors (KNN).
Impact of Not Applying Standardization and Min-Max Scaling
If feature scaling is not applied, models like Linear Regression and Logistic Regression can perform sub optimally. These models are sensitive to the scale of the input features. Here’s how the lack of scaling can impact them:
1. Weight Interpretation and Coefficients:
In Linear and Logistic Regression, the model coefficients (weights) are directly influenced by the scale of the features. If the features have vastly different scales, the model might place disproportionate emphasis on features with larger scales, leading to biased or misleading results. For instance, a feature measured in thousands could dominate another feature measured in single digits, even if the latter is more predictive.
2. Convergence of Gradient Descent:
Gradient Descent, the optimization algorithm used to minimize the cost function in these models, can struggle to converge if the features are not scaled. Features with larger ranges can cause the gradient to oscillate, leading to slower convergence or even failure to reach the optimal solution.
3. Model Performance:
Without scaling, the model might perform poorly, especially on test data, as it may not generalize well. The differences in feature scales can lead to an inefficient exploration of the parameter space, resulting in suboptimal model parameters.
Models That Do Not Require Standardization or Min-Max Scaling
Some models are inherently insensitive to feature scaling. These models either do not rely on distances or ratios of the input features, or they incorporate scaling as part of their internal calculations:
- Decision Trees: Algorithms like Decision Trees, Random Forests, and Gradient Boosting Trees do not require feature scaling. These models split nodes based on feature thresholds and are not affected by the scale of the features.
- Naive Bayes: This algorithm assumes independence between features and is not affected by their scale.
- Rule-Based Models: Models like RuleFit or other rule-based learning methods do not require scaling as they are based on logical conditions rather than numerical calculations involving distances.
Use Cases in Machine Learning and Deep Learning
Standardization:
- Machine Learning: Logistic Regression, SVM, PCA, and Linear Regression.
- Deep Learning: Useful in regularized models or algorithms where the data’s distribution matters.
Min-Max Scaling:
- Machine Learning: K-Nearest Neighbors (KNN), clustering methods like K-Means, and any algorithm where the data range affects the performance.
- Deep Learning: Essential in Neural Networks, especially with activation functions like Sigmoid or Tanh, requiring inputs within a specific range.
Python Code Implementation
Below is a Python implementation using the scikit-learn library to demonstrate both Standardization and Min-Max Scaling.
import numpy as np
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# Example dataset: students' scores
scores = np.array([[85],
[90],
[75],
[60],
[95]])
# Standardization
scaler_standard = StandardScaler()
scores_standardized = scaler_standard.fit_transform(scores)
print("Standardized Scores:")
print(scores_standardized)
# Min-Max Scaling
scaler_minmax = MinMaxScaler()
scores_minmax_scaled = scaler_minmax.fit_transform(scores)
print("\nMin-Max Scaled Scores:")
print(scores_minmax_scaled)Output:
The output shows the transformed scores for both methods:

Conclusion
Feature scaling is crucial in preparing data for machine learning and deep learning models. While Standardization and Min-Max Scaling serve similar purposes, they are applied in different contexts based on the algorithm’s requirements and the data’s characteristics. Not applying these techniques to models like Linear Regression and Logistic Regression can lead to poor performance, slow convergence, and biased results. However, some models like Decision Trees and Naive Bayes do not require scaling. Understanding these techniques and their applications can significantly improve model performance and accuracy.